Paper Info
Submit Date: Feb 15, 2018
Introduction
word2vec이나 glove와 같은 기존의 word embedding 방식은 다의어의 모든 의미를 담아내기 곤란하다는 심각한 한계점을 갖고 있다. ELMo(Embeddings from Language Models)는 이러한 한계점을 극복하기 위해 embedding에 sentence의 전체 context를 담도록 했다. pre-train된 LSTM layer에 sentence 전체를 넣어 각 word의 embedding을 구해내는 model이다. 이로 인해 기존의 embedding에 비해 복잡한 syntax, semantic한 특징들을 담아낼 수 있었고, 다의어 문제도 해결했다. LSTM은 forward, backward 2가지 방향을 사용하는데 각 LSTM은 다음 word를 예측하는 model이다. 이러한 LSTM layer를 다층으로 구성해 context-dependent한 word embedding을 생성해내게 된다. ELMo를 사용한 word embedding은 수많은 NLP task에서 성능 향상을 이끌어낼 수 있다.
ELMo: Embeddings from Language Models
ELMo와 여타 word embedding model과의 가장 큰 차이점은 각 단어마다 고정된 word embedding을 사용하는 것이 아닌 pre-trained model 자체를 하나의 function 개념으로 사용한다는 것이다. 이전의 word2vec 등은 model을 train시킨 뒤 각 word마다의 embedding vector만을 추출해 사용했지만, ELMo는 word마다 embedding vector가 특정되지 않기에 이와 같은 방식이 불가능하고, ELMo model을 NLP model의 앞에 연결하는 방식으로 사용하게 된다.
Bidirectional language models
input sequence가 \(N\)개의 token들 (\(t_1, t_2, ..., t_N\))이라고 가정하자. \(t_k\)는 모두 각 word에 대한 context-independent token이다.
forward LSTM은 \(t_1, ... , t_{k-1}\)이 주어졌을 때 \(t_k\)를 예측하는 model이다.
\(j\)번째 LSTM layer에서 \(k\)번째 token에 대한 forward LSTM output은 \(\overrightarrow{h}_{k,j}\)이다. 마지막 LSTM layer의 output인 \(\overrightarrow{h}_{k,L}\)을 softmax에 넣어 최종적으로 \(t_{k+1}\)을 예측하게 된다.
\[p(t_1, t_2, ... , t_N) = \prod^N_{k=1}{p(t_k \vert t_1, t_2, ..., t_{k-1})}\]backward LSTM은 \(t_{k+1}, t_{k+2}, ... ,t_N\)이 주어졌을 때 \(t_k\)를 예측하는 model이다.
\(j\)번째 LSTM layer에서 \(k\)번째 token에 대한 backward LSTM output은 \(\overleftarrow{h}_{k,j}\)이다. 마지막 LSTM layer의 output인 \(\overleftarrow{h}_{k,L}\)을 softmax에 넣어 최종적으로 \(t_{k-1}\)을 예측하게 된다.
\[p(t_1, t_2, ... , t_N) = \prod^N_{k=1}{p(t_k \vert t_{k+1}, t_{k+2}, ..., t_{N})}\]biLM은 위의 두 LSTM을 결합한 것이다. 두 방향에 대한 log likelihood를 최대화하는 것을 목표로 한다.
\[\sum^N_{k=1} {(\log p(t_k \vert t_1, ... , t_{k-1} ; \Theta_x, \overrightarrow{\Theta}_{\text{LSTM}}, \Theta_s) + \log p(t_k \vert t_{k+1}, ... , t_{N} ; \Theta_x, \overleftarrow{\Theta}_{\text{LSTM}}, \Theta_s))}\]\(\Theta_x\)는 token representation(\(t_1, ... , t_N\))에 대한 parameter이고, \(\Theta_s\)는 softmax layer에 대한 parameter이다. 이 두 parameter는 전체 direction에 관계 없이 같은 값을 공유하지만, LSTM의 parameter들은 두 LSTM model이 서로 다른 값을 갖는다.
ELMo
ELMo에서는 새로운 representation을 사용하는데, 이를 얻기 위해서는 LSTM layer의 개수를 \(L\)이라고 했을 때 총 \(2L+1\)개의 representation을 concatenate해야 한다. input representation layer 1개와 forward, backward LSTM 각각 \(L\)개이다.
\[R_k = \{x_k, \overrightarrow{h}_{k,j}, \overleftarrow{h}_{k,j} \vert j=1, ... , L\}\]input representation layer를 \(j=0\)으로, \(\overrightarrow{h}_{k,j}\)와 \(\overleftarrow{h}_{k,j}\)의 concatenation을 \(h_{k,j}\)로 표현한다면 다음과 같은 일반화된 수식으로 ELMO representation을 표현할 수 있다.
\[R_k = \{h_{k,j} \vert j=0, ..., L\}\]결국 \(R_k\)는 \(k\)번째 token에 대한 모든 representation이 연결되어 있는 것인데, 이를 사용해 최종 ELMo embedding vector를 만들어내게 된다.
\[\text{ELMo}^{task}_k=E(R_k;\Theta^{task}) = \gamma^{task} \sum^L_{j=0} {s_j^{task}h_{k,j}}\]각 LSTM layer의 output인 \(h_{k,j}\)를 모두 더하는데 이 때 각각에 softmax-normalized weights \(s_j\)를 곱한 뒤 더하게 된다. 당연하게도 \(\sum^L_{j=0}s_j^{task}=1\)이다. 마지막에 최종적으로 \(\gamma\)를 곱하게 되는데, scale parameter이다. \(s_j\)와 \(\gamma\)는 모두 learnable parameter이면서 optimization에서 매우 중요한 역할을 담당한다.
Using biLMs for supervised NLP tasks
supervised downstream task에 ELMo를 적용하는 구체적인 방법은 간단하다. 대부분의 supervised NLP model들의 input은 모두 context-independent token들의 sequence이다. 이러한 공통점 덕분에 동일한 방법으로 대부분의 task에 ELMo를 적용할 수 있다. 우선 NLP model의 input layer와 다음 layer 사이에 ELMo를 삽입한다. 이후 ELMo 이후 layer에서는 input을 \([x_k;\text{ELMo}_k^{task}]\)로 사용한다. 즉, input token과 ELMo embedding vector의 concatenation을 사용하는 것이다. NLP model을 train할 때에는 ELMo의 weight들은 모두 freeze시킨다. 즉, ELMo model은 NLP model이 train될 때 함께 train되지 않는다.
SNLI, SQuAD와 같은 특정 task에서는 RNN의 output \(h_k\)를 \([h_k;\text{ELMo}_k^{task}]\)로 교체했을 때 더 좋은 성능을 보이기도 했다. 또한 일반적으로 dropout과 \(\lambda \Vert w \Vert^2_2\)를 loss에 더하는 regularization을 사용했을 때 더 좋은 성능을 보였다.
Pre-trained bidirectional language model architecture
ELMo는 기존의 pre-trained biLM와 큰 구조는 비슷하지만 몇가지 차이점이 존재하는데, 가장 큰 차이점은 LSTM layer 사이에 residual connection을 사용했다는 점이다. 이를 통해 input의 feature를 더 잘 전달하고 gradient vanishing을 해결할 수 있다. \(L=2\)개의 biLSTM layer를 사용했고, 4096개의 unit과 512차원의 projection을 사용했다. biLSTM의 input으로는 2048 character n-gram을 CNN에 넣는 char-CNN embedding을 사용했다.
Evaluation
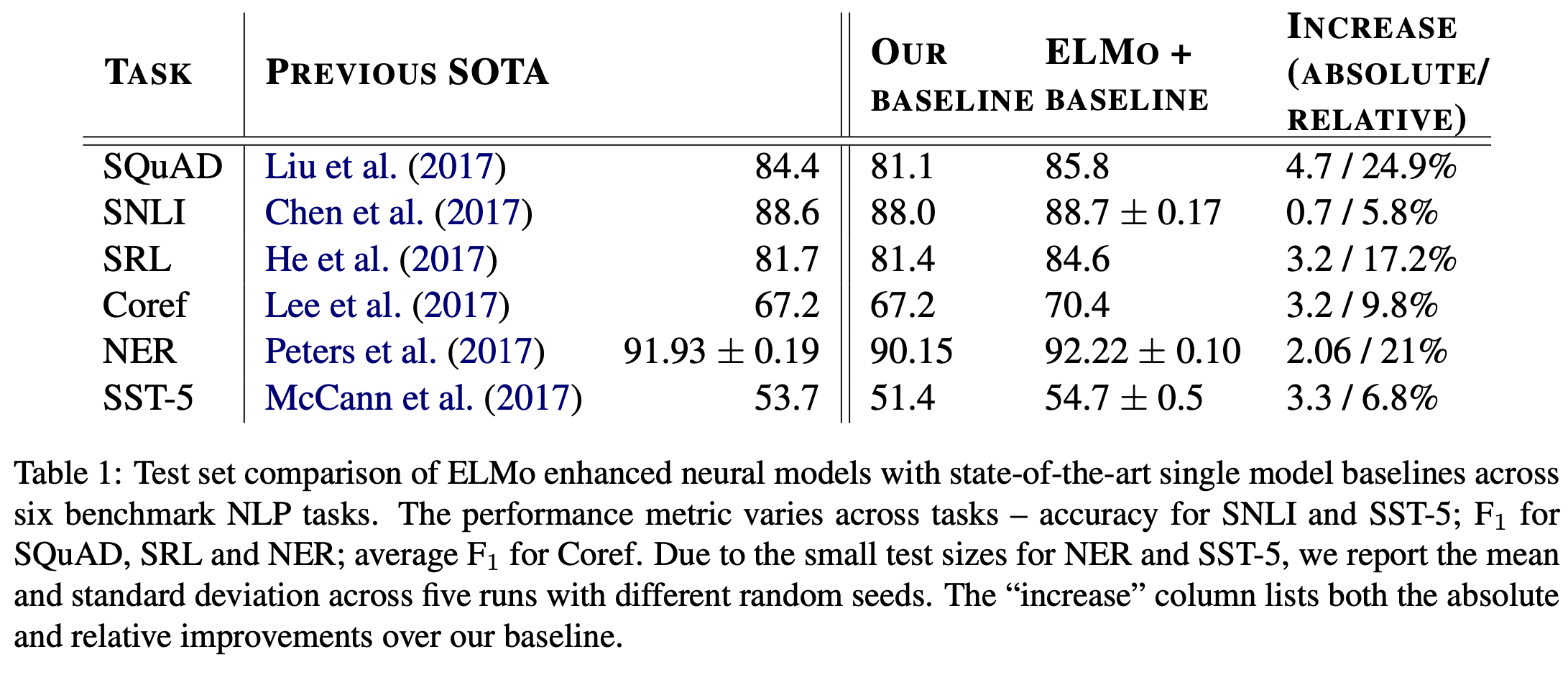
ELMo를 단순하게 추가하는 것만으로도 baseline model에 비해 성능이 향상됐고, 이를 통해 SOTA를 달성할 수 있었다.
Analysis
Alternate layer weighting schemes
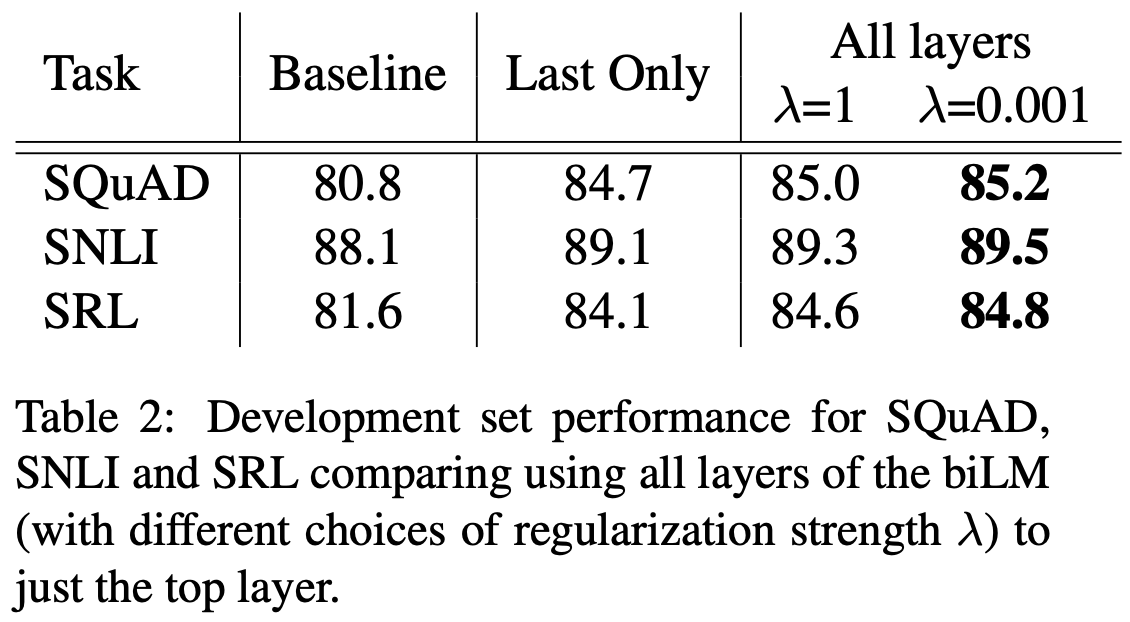
ELMo representation을 사용하지 않고 단순하게 LSTM의 마지막 layer의 output (\(h_{k,L}\))을 사용하는 방법도 있다. 이러한 방식은 biLM, CoVe 등 기존의 많은 연구에서 시도되었는데 이와 ELMo representation을 사용한 경우를 비교해본다. Table 2의 Last Only는 마지막 LSTM layer의 output만을 word embedding으로 사용하는 경우이다.
\(\lambda\)는 softmax-normalized weights \(s_j\)에 대한 regularization parameter인데, 0~1 사이의 값을 갖는다. \(\lambda\)가 1에 가까울수록 각 layer에서의 output들을 평균에 가깝게 계산해 최종 vector를 생성해내고 (\(s_j\)가 모두 유사한 값), \(\lambda\)가 0에 가까울수록 각 layer에서의 output들에 다양한 값들이 곱해서 더해진다.
Table 2에서는 task에 관계 없이 동일한 경향성을 보이는데, baseline model보다 CoVe와 같은 마지막 LSTM layer의 output을 word embedding으로 사용한 model이 더 좋은 성능을 보였다. 또한 CoVe보다 ELMo가 더 좋은 성능을 보였는데, 이 중 \(\lambda\)가 낮은 경우가 더 좋은 결과를 보였다.
Where to include ELMo?
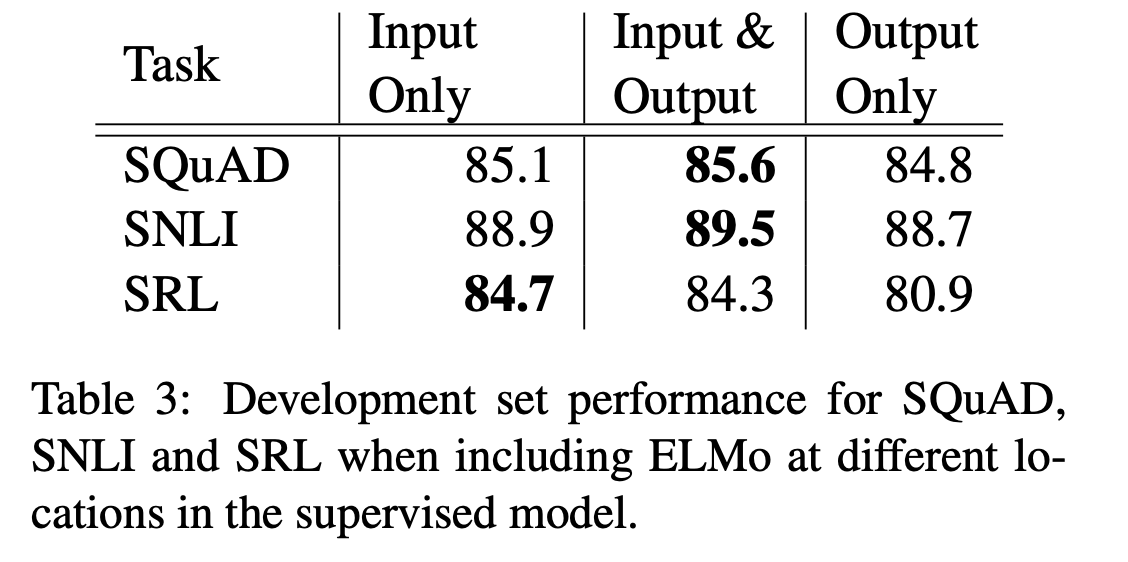
위에서 언급했듯 supervised NLP model에 ELMo를 적용할 때에는 input layer의 직후에 ELMo를 삽입했다. SQuAD, SNLI, SRL의 baseline model은 모두 biRNN model인데, ELMo를 biRNN 직후에도 삽입을 한 뒤 성능을 비교했다. SQuAD와 SNLI에 있어서는 ELMo를 biRNN 이후에도 추가하는 것이 더 좋은 성능을 보여줬는데, 이는 SNLI와 SQuAD는 biRNN 직후 attention layer가 있는데, biRNN과 attention layer 사이에 ELMo를 추가함으로써 ELMo representation에 attention이 직접적으로 반영됐기 때문이라고 유추해 볼 수 있다.
What information is captured by the biLM’s representations?

Word sense disambiguation
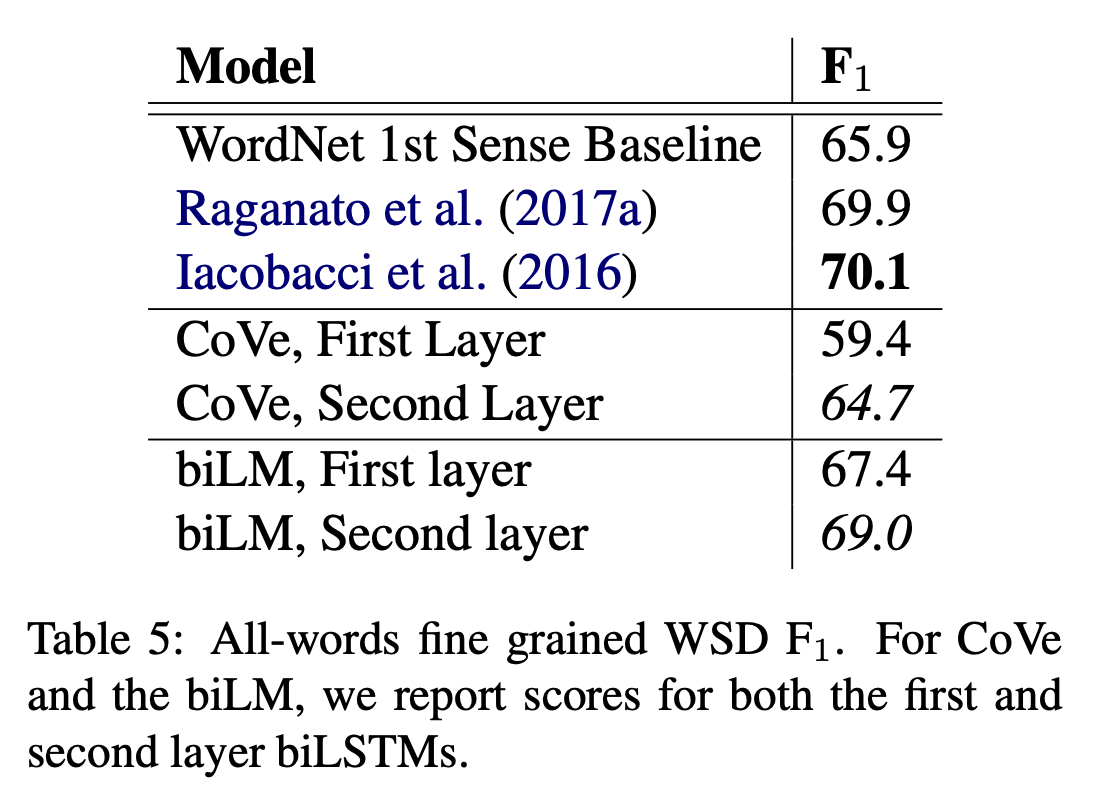
WSD는 다의어의 의미를 구분짓는 task로 embedding이 얼마나 semantic 정보를 잘 담고 있는지에 대한 지표이다. ELMo는 WSD-specific한 model과 동등한 수치를, CoVe보다는 월등히 높은 수치를 달성했다. 주목할만한 점은 ELMo의 first LSTM layer의 output보다는 second layer (top layer)의 output이 WSD에서 좋은 성능을 보였다는 점이다.
POS tagging
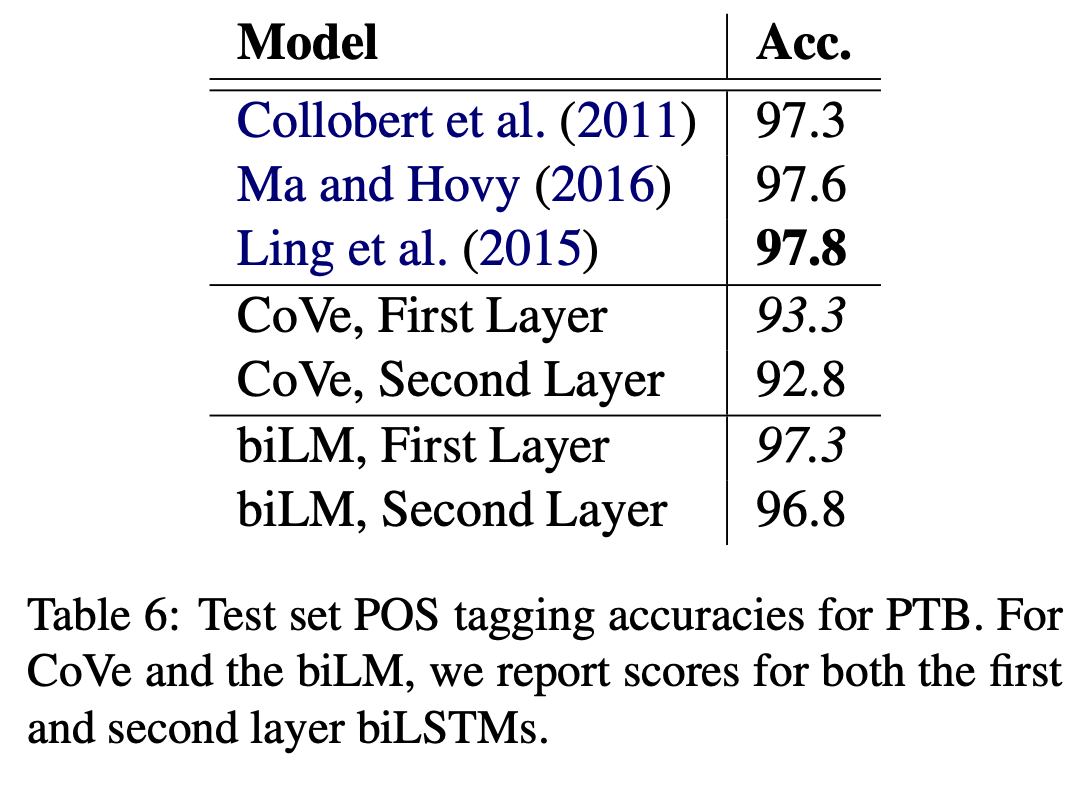
POS tagging은 word의 품사를 tagging하는 task로 embedding이 얼마나 syntax 정보를 잘 담고 있는지에 대한 지표이다. 여기서도 ELMo는 POS tagging-specific model과 동둥한 수준의 성능을, CoVe보다는 월등히 높은 성능을 보여줬다. WSD와는 다르게 오히려 first LSTM layer의 output이 top layer의 output보다 POS tagging에서 더 좋은 성능을 보였다는 점이 주목할 만하다.
Implications for supervised tasks
결론적으로 ELMo에서 각 layer는 담고 있는 정보의 종류가 다르다고 할 수 있는데, 층이 낮은 layer(input layer에 가까운 layer)일수록 syntax 정보를, 층이 높은 layer(output layer에 가까운 layer)일수록 semantic 정보를 저장한다.
Sample efficiency
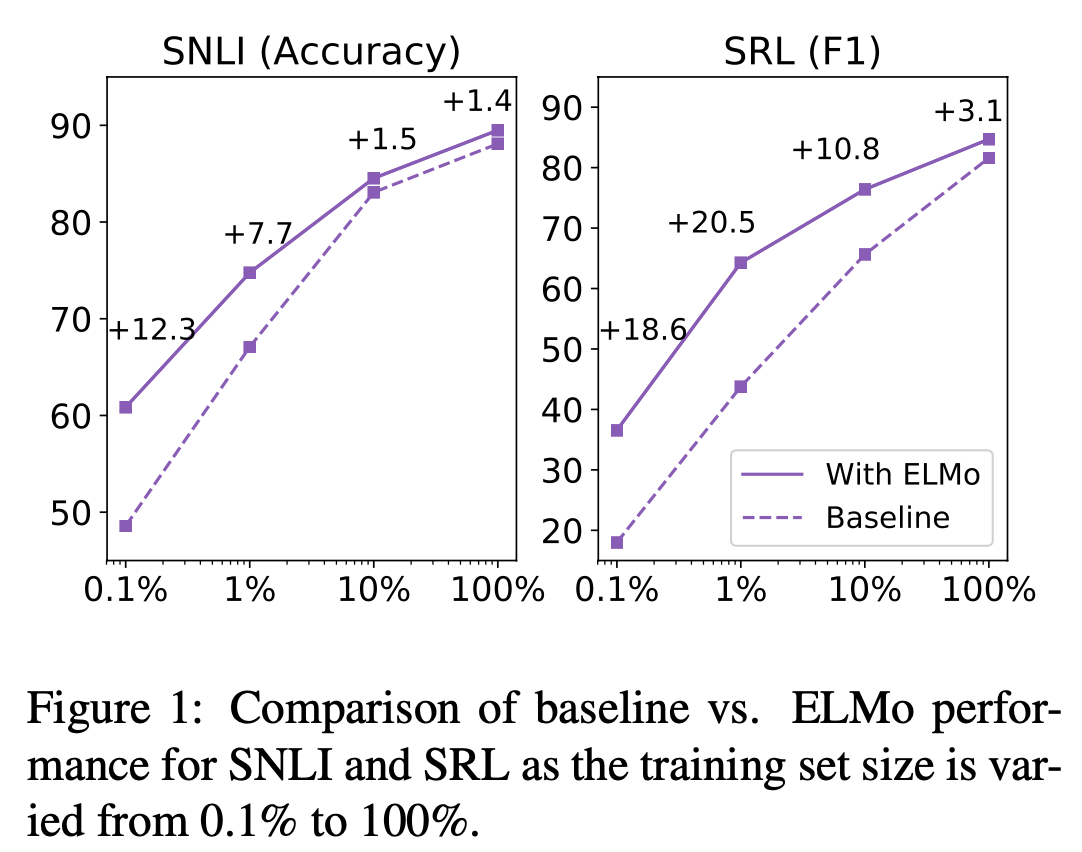
ELMo의 사용은 일정 수준 이상의 성능 달성에 필요한 parameter update 횟수 및 전체 training set size를 획기적으로 줄여준다. SRL task에 있어서 ELMo 사용 이전 baseline model의 경우에는 486 epoch가 지나서야 score가 수렴했는데, ELMo를 추가하고 난 뒤에는 10 epoch만에 baseline model의 score를 능가했다.
Figure 1에서는 같은 크기의 dataset에서 ELMo를 사용하는 경우가 훨씬 더 좋은 성능을 낸다는 것을 보여준다. 심지어 SRL task에서는 ELMo를 사용한 model이 training dataset의 단 1%을 학습했을 때 달성한 수치와 baseline model이 training dataset의 10%를 학습했을 때의 수치가 동일하다는 것을 확인할 수 있다.
Visualization of learned weights
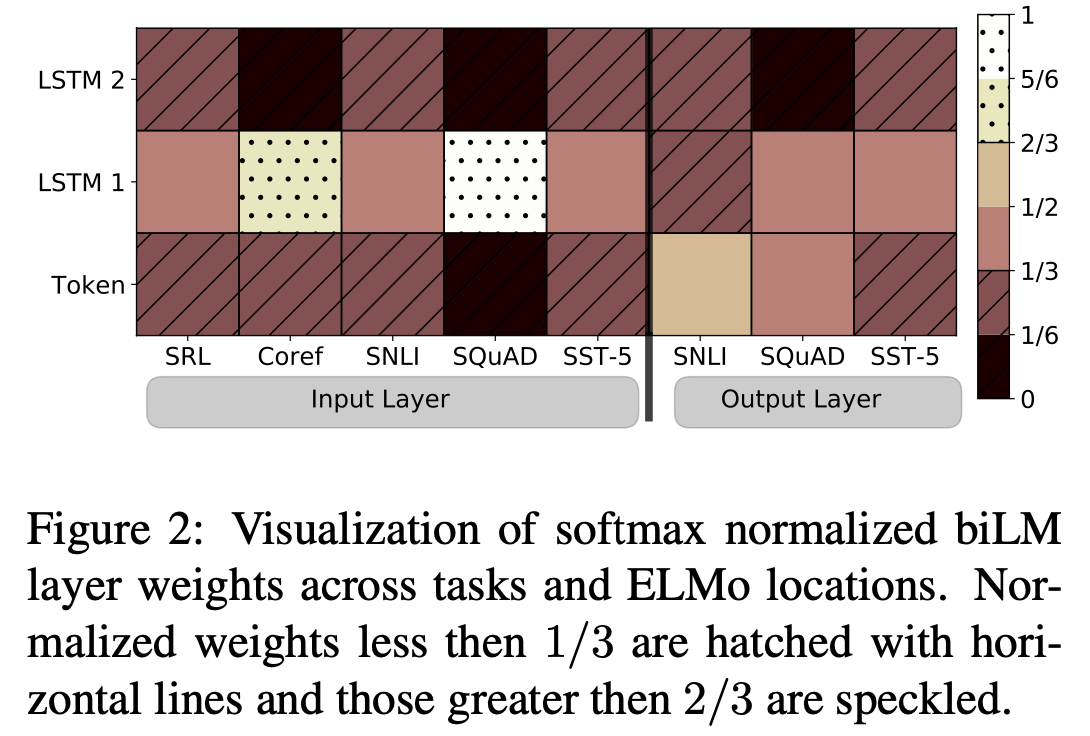
softmax-normalized parameter \(s_j\)를 시각화한 것이다. ELMo를 biRNN의 input과 output에 사용했을 때를 각각 나눠 비교했다. ELMo가 input에 사용된 경우에는 대개 first LSTM layer가 선호되는 경향을 보였다. 특히나 SQuAD에서 이러한 경향성이 가장 두드러지게 나타났다. 반면 ELMO가 output에 사용된 경우에는 weight가 균형있게 분배되었지만 낮은 layer가 조금 더 높은 선호를 보였다.
Conclusion
biLM을 사용해 높은 수준의 context를 학습하는 ELMo model을 제안했다. ELMo model을 사용하면 대부분의 NLP task에서 성능이 향상되었다. 또한 layer의 층이 올라갈수록 syntax보다는 semantic한 정보를 담아낸다는 사실도 발견해냈다. 때문에 어느 한 layer를 사용하는 것보다는 모든 layer의 representation을 결합해 사용하는 것이 전반적인 성능 향상에 도움이 된다는 결론을 내릴 수 있다.