Paper Info

Archive Link

Paper Link

Submit Date: Sep, 16, 2020

---

Introduction

NLP에서 Transformer가 현재 대세임은 누구도 부정할 수 없다. WMT19의 NMT task에 제출된 model의 약 80%가 Transformer 기반이라는 통계도 있을 정도로 Transformer는 널리 사용되고 있다. 하지만 Transformer는 그 특성 상 많은 memory가 필요하고 연산량이 많기에 mobile device에서 deliver되기에는 제약이 많다. 이를 해결하기 위해 model 경량화 중 quantization에 대한 많은 기존의 연구가 있어왔으나 그 대부분은 model 전체에서 동일한 quantization 전략을 채택했다는 한계가 있다. 본 논문은 이에 더 나아가 Transformer에 최적화된 mixed precision quantization전략을 제시한다. Transformer의 특징을 분석해 각각의 module에 적절한 precision을 정해 module마다 다른 quantization precision을 적용하는 것이다. 대표적으로 embedding block에서는 각 word의 통계 기반 중요도를 정해 precision에 반영하고, encoder-decoder block에서는 sub-layer의 sensitivity를 기준으로 precision을 정한다. 이러한 방식을 finer-grained mixed precision approach라고 명명한다. 이를 통해 최대 3bit 미만의 precision을 갖는 경우도 생기게 된다. 본 논문에서 제시한 quantization이 적용된 Transformer model은 baseline 대비 11.8배 작으면서 0.5 BLEU Score만이 감소했고, run-time memory는 8.3배 작았으며, mobile device(Galaxy Note 10+)에서 3.5배 빠른 inference speed를 보여줬다.

Background

Transformer

Transformer는 크게 encoder, decoder, embedding으로 구분되는데 #parameters를 기준으로 비율을 측정한다면 각각 31.0%, 41.4%, 27.6%이다. embedding block은 단순히 하나의 weight matrix인데, 이 matrix의 각 row는 하나의 단어를 의미했다. 하지만 auto-regressive한 연산 때문에 실제 연산량과 #parameters의 비율을 동일시 할 수는 없다. 한편, Transformer의 세 module의 memory 사용량 및 속도를 비교하려면, encoder와 decoder의 특성을 이해해야 한다. encoder는 높은 수준의 parallelism이 가능한 반면, decoder는 결국 decoder에서 token을 1개 씩 생성하고 이 token이 다음 decoder 실행에 입력으로 들어오기 때문에 낮은 수준(decoder layer 수준)의 parallelism밖에 할 수 없다. 따라서 decoder에서는 cache 사용량이 더 많고 연산 속도도 더 느리다.

Non-uniform Quantization Based on Binary-codes

uniform quantization은 full precision parameters를 \(2^q\)로 표현할 수 있는 unsigned 값 (0 ~ \(2^q - 1\))으로 mapping하는 것이다. 이 때 \(q\)는 quantization bit의 개수, 즉 precision을 의미한다. precision이 낮을수록 곱셈, 덧셈 등의 연산에서 cost가 감소하지만, 이는 연산에 사용되는 모든 값들이 quantized되었을 때에만 유효하다. 또한 과도한 outlier 값이 포함된 경우에는 quantization error가 매우 높아진다는 한계점도 존재한다.

non-uniform quantization는 크게 codebook-based와 binary-code based로 구분되는데, 본 논문에서는 binary-code based를 채택했다. binary-code based quantization은 full precision vector \(w\in R^p\)를 \(\sum^q_{i=1}\alpha_i b_i\)로 mapping시키는 것이다. 이 때 \(\alpha_i \in R\)는 scailing factor, \(b_i \in \{-1,+1\}^p\)는 binary vector이다. \(p\)는 vector \(w\)의 길이를, \(q\)는 quantization bits의 개수를 의미한다. scailing vector와 binary vector는 모두 아래와 같은 argmin 수식을 통해 구해진다.

\[argmin_{a_i, b_i}\left\lVert w - \sum^q_{i=1}\alpha_i b_i \right\rVert^2\]

quantization error를 줄이기 위해서는 heuristic한 approach가 사용되는데, 예를 들어 matrix quantization이라고 할 경우 matrix의 row, column vector들이 사용된다.

Quantization Strategy for Transformer

Transformer에 적합한 non-uniform quantization bits를 찾는다. 우선 Transformer를 Embedding block과 Encoder and Decoder block로 구분해 접근을 다르게 했는데, Embedding block에서는 각 단어의 등장 빈도를 고려했고, Encoder and Decoder block에서는 각 sub-layer type에 대해 알맞은 가장 작은quantization bits를 구했다. 이 때 BLEU score를 갖고 test를 진행해 결론을 도출해냈다.

Embedding

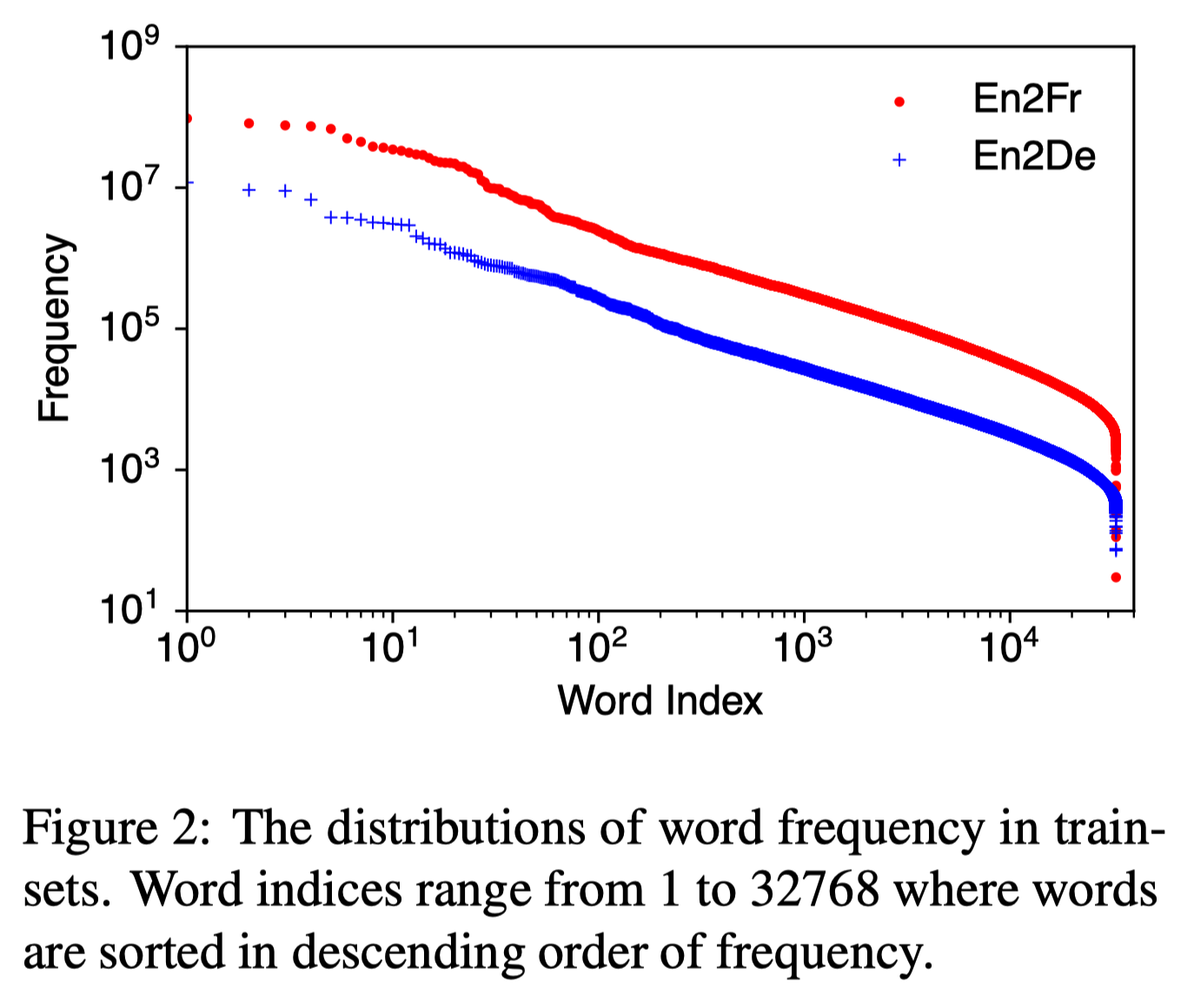
각종 dataset에서 단어 등장 빈도를 조사해보면, language에 관계 없이 공통적으로 매우 적은 수의 단어가 전체 단어 등장 빈도의 대부분을 차지하는 경향성을 보인다. 실제로 Figure2를 확인해보면 WMT14 dataset에서는 En2Fr, En2De등 language에 관계 없이 고작 1%의 단어가 전체 단어 등장 빈도의 95%를 cover했다. 이런 심각한 비대칭성을 보임에도 일괄적으로 모든 단어에 동일한 quantization을 적용한다면 등장 빈도가 매우 높은 소수의 단어들에서 정보의 손실이 많이 발생할 것이다. 본 논문에서는 이를 해결하기 위해 명확한 원칙을 정했다. 등장 빈도가 높은 단어들은 quantization bit를 많이 부여하고, 등장 빈도가 낮은 단어들에 대해서 quantization bit를 적게 부여하는 것이다. 정보 이론의 entropy 개념을 적용해보면, entropy가 높은 단어들은 압축을 많이, entropy가 낮은 단어들은 압축을 적게 한다고 볼 수 있다. 아래는 이러한 원칙을 적용해 단어들을 빈도 기준으로 clustering해 다른 quantization 정책을 적용하는 algorithm이다.

\(v\)는 단어의 개수, \(d_{model}\)은 embedding dimension이다. \(b\)는 #clusters이고, \(r\)은 각 cluster마다 담을 단어의 개수를 정하는 factor이다. 한 행 씩 분석해보자.

• 1행에서는 word vector들을 등장 빈도 기준으로 내림차순 정렬한다.
• 2~3행에서는 \(i\)를 \(0\)부터 \(b-1\)까지 반복, 즉 cluster를 탐색한다.

• 4행에서는 \(r\)과 \(v\)를 사용해 현재(\(i\)번째) cluster에 저장할 단어의 개수(\(c^i_{size}\))를 구한다.

  \[c^i_{size} = \frac{v}{\sum^{b-1}_{k=0}r^k} \cdot r^i\]

  \(r^i\)의 비율을 \(v\)에 곱하는 식이다. cluster의 index가 증가할 때마다 담는 단어의 개수를 늘린다.

• 5행에서는 현재(\(i\)번째) cluster에서 사용할 #quantization bits(\(c^i_{bit}\))를 구한다. 단순하게 \(b - i\)이다.
• 6~10행에서는 현재(\(i\)번째) cluster에 담을 단어들을 각각 quantize한다.

\(b=4\), \(r=2\)인 경우의 예시에 대해서 살펴보자.

\(r^0=1,\ r^1=2,\ r^2=4,\ r^3=8\)이다. 따라서 \(\sum^{b-1}_{k=0}r^k=15\)이다.

단어의 개수(\(v\))가 1500개라고 가정해보자.

\(c^0_{size}=100, c^1_{size}=200, c^2_{size}=400, c^3_{size}=800\)일 것이다.

\(c^0_{bits}=4,\ c^1_{bits}=3,\ c^2_{bits}=2,\ c^3_{bits}=1\)이다.

이는 직관적으로 이해하자면 상위 \(\frac{1}{15}\)개의 단어에 대해서는 4bit로, 이후 상위 \(\frac{2}{15}\)개의 단어에 대해서는 3bit로, 이후 상위 \(\frac{4}{15}\)개의 단어에 대해서는 2bit로, 나머지 \(\frac{8}{15}\)를 차지하는 단어에 대해서는 1bit로 압축하는 것이다.

이러한 algorithm은 결국 대부분의 단어를 단지 1~2bit만으로 표현을 하게 되는 것이다. \(b=4\), \(r=8\)인 경우에는 무려 87.5%의 단어들이 1bit로 quantize된다. 하지만 이런 quantization을 적용한다 하더라도 uniform quantization과 비교하면 성능 하락은 크지 않다. 오히려 적절한 quantization 값을 선택할 경우 평균 #quantization bits가 더 작은 상황에서도 uniform quantization에 비해 성능이 높게 나오기도 한다.

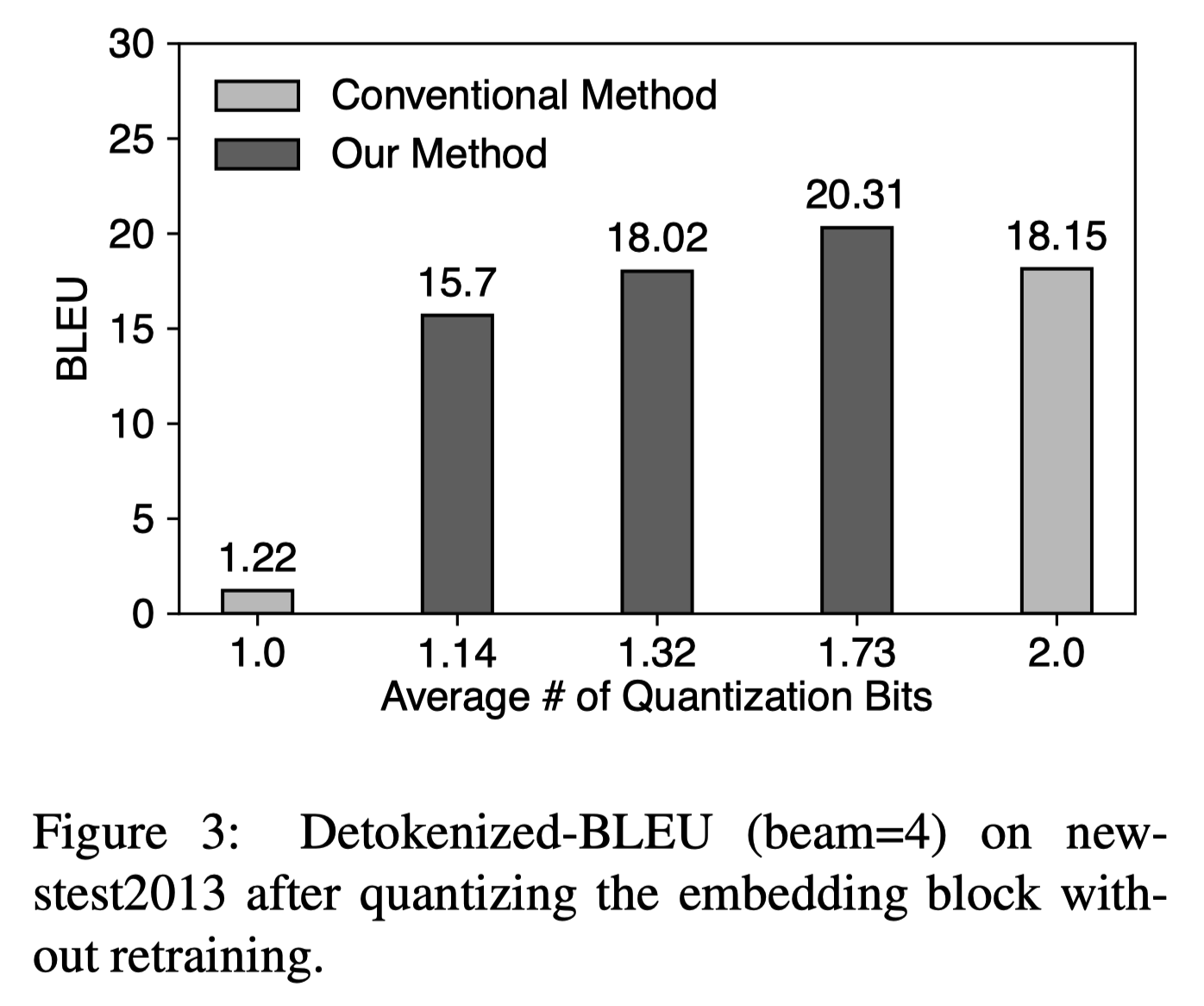
\(b=4\)인 경우에 대해 각각 \(r=8, r=4, r=2\)인 경우로 BLEU Score를 측정해 uniform quantization과 비교했다. \(r=2\)인 경우에는 평균 #quantization bits는 1.73이지만 2bits uniform quantization에 비해 오히려 높은 성능을 보였다.

Encoder and Decoder

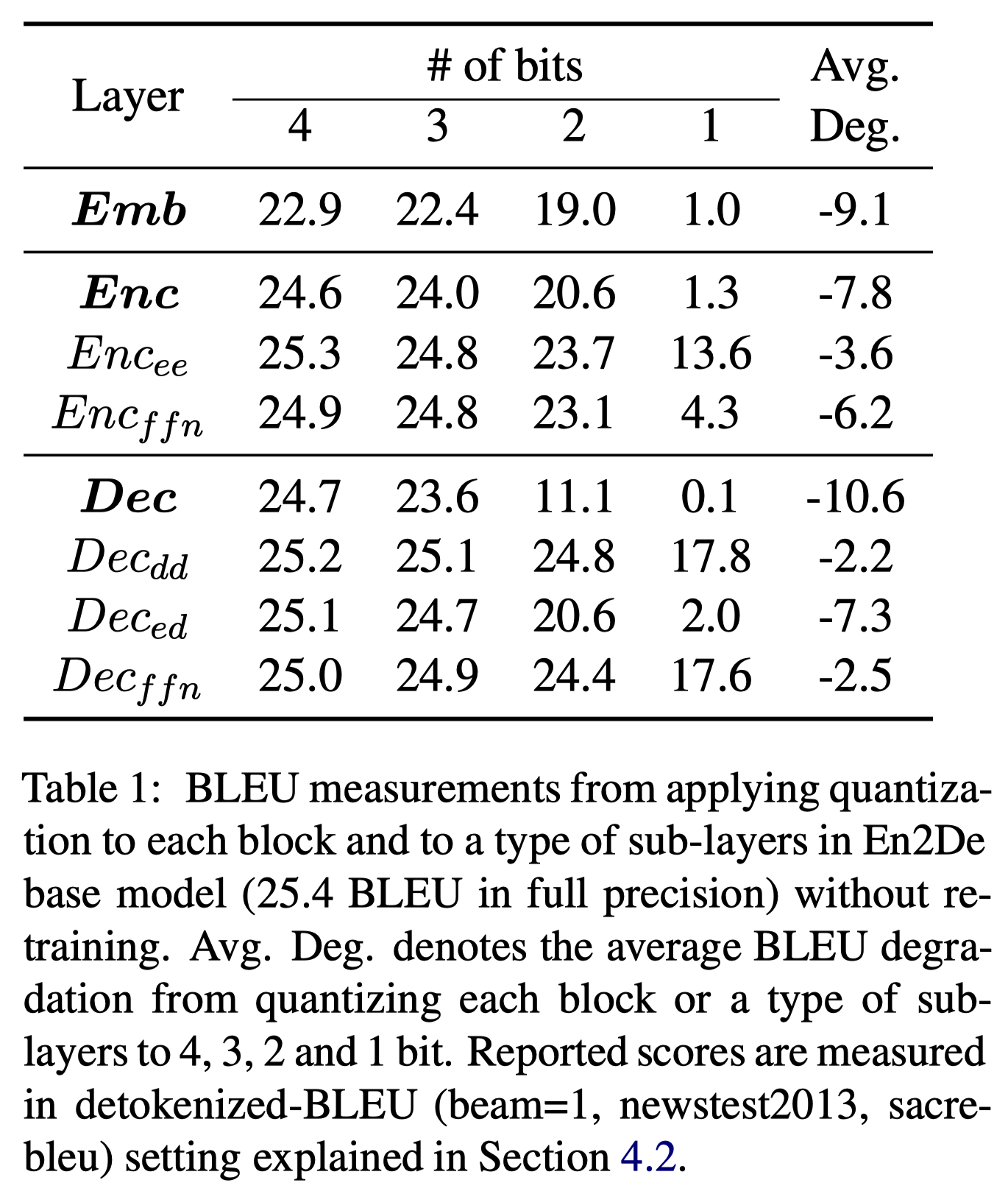
Transformer의 각 sub-layer들 중 어떤 layer들이 quantization에 민감한지 알아보는 연구를 진행했다. Transformer의 layer는 크게 Embedding block, Encoder block, Decoder block으로 구분한다. 이 중 Embedding block에 대해서는 위에서 다뤘기에 생략하고, Encoder, Decoder block에 집중한다. encoder block은 encoder-encoder(self-attention) layer \(Enc_{ee}\), ffn(feed-forward) layer \(Enc_{ffn}\)로 구성되고, decoder block은 decoder-decoder(self-attention) layer \(Dec_{dd}\), encoder-decoder layer \(Dec_{ed}\), ffn(feed-forward) layer \(Dec_{ffn}\)로 구성된다.

가장 quantization에 민감한 반응을 보인 sub-layer는 \(Dec_{ed}\)였다. encoder와 decoder 사이에 전달되는 정보가 전체 Transformer에서 가장 중요한 부분임을 생각하면 당연한 결과이다. 심지어 \(Dec_{ffn}\)의 경우에는 \(Dec_{ed}\)보다 #parameters는 2배나 컸음에도 불구하고 \(Dec_{ed}\)가 더 민감하게 반응했다. Encoder에서는 \(Enc_{ffn}\)이 \(Enc_{ee}\)보다 더 민감하게 반응했다. 본 논문에서는 이러한 quantization 민감도 관점을 반영해 각 sub-layer에 적절한 수치를 찾아나간다.

위와 별개로 Transformer의 auto-regressive한 특성 때문에 발생하는 decoder의 parallelism 어려움 역시 고려하게 된다. 이와 같은 이유로 실제 inference time에서는 decoder가 더 많은 비중을 차지하기 때문에 decoder에는 encoder 대비 더 적은 quantization bit를 부여하게 된다.

Experiments

Quantization Details

Methodology

Greedy approximation algorithm을 사용했다.

Retraining Details

3단계의 retraining을 수행한다. 각 단계는 embedding block, decoder block, encoder block을 quantization하기 위함이다. decoder block이 encoder block보다 먼저 retraining된다는 점을 기억하자.

Quantized Parameters

weight는 모두 quantization하지만, bias vector나 layer normalization parameter는 quantization 대상에서 제외한다. 이 parameter들은 전체 #parameters에서 아주

Experimental Settings

Dataset

En2De, En2Fr, En2Jp의 3가지 language 번역 task에 대해서 test를 진행했다. En2De와 En2Fr에 있어서는 WMT14를 trainset으로, newstest2013을 devset으로, newstest2014를 testset으로 했다. En2Jp에서는 KFTT, JESC, WIT dataset을 사용했는데, trainset과 devset은 3가지 dataset의 것들을 모두 결합해 사용했고, testset은 KFTT의 testset을 사용했다.

BLEU

Results

Translation Quality

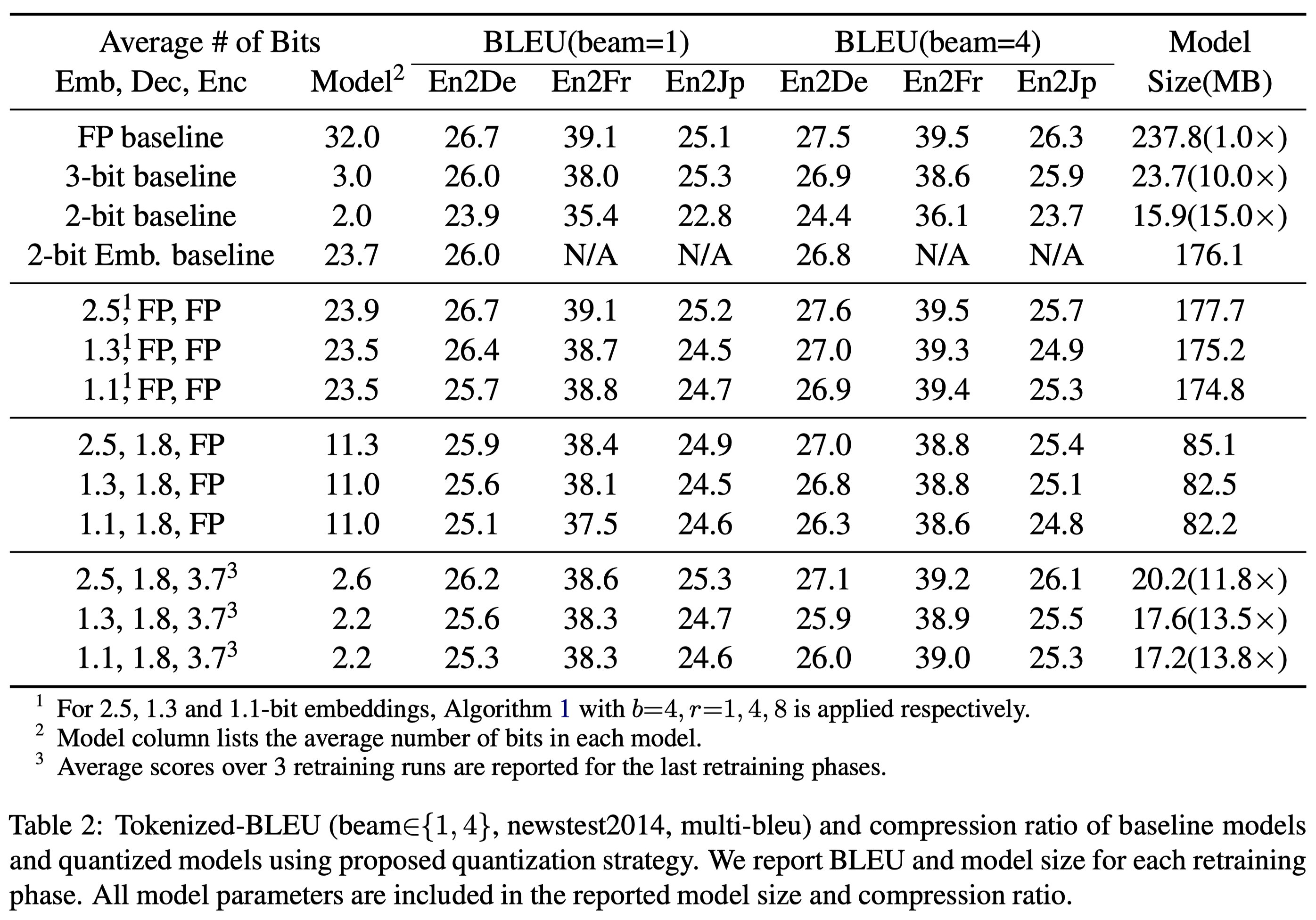
baseline Transformer model을 4가지 방식으로 quantization을 수행했다. FP는 full-precision(quantization 수행하지 않음)이고, 3-bit, 2-bit는 각각 3, 2bit로 quantization을 수행한 것이다 .2-bit Emb는 기본적으로 FP이나 embedding block에 대해서만 2bit quantization을 수행한 것이다.

Model column은 전체 평균 quantization bit를 의미한다. column이 beam=1, beam=4로 구분되어져 있는데, beam=1은 \(b=1\)인 경우, 즉 uniform quantization이다. 반면 beam=4는 \(b=4\)인 non-uniform quantization이다.

baseline을 제외하고는 모두 non-uniform quantization을 수행한 것인데, 총 3개의 숫자로 표현된다. 각각 embedding block, decoder block, encoder block의 평균 quantization bits이다. 이 중 embedding block을 살펴보면 모두 \(b=4\)이고, \(2.5\)는 \(r=1\), \(1.3\)은 \(r=4\), \(1.1\)은 \(r=8\)인 경우이다.

embedding block, decoder block, encoder block을 위해 총 3번 (re)training을 수행했고, 표의 각 row가 세 block들을 위한 training step을 의미한다. encoder block보다 decoder block에 대한 retraining이 먼저 수행됨을 명심하자.

1. Embedding block

   (1.1, FP, FP)는 대략 2-bit Embedding baseline과 유사한 성능을 보인다. 1.3-bit embedding, 1.1-bit embedding을 수행했음에도 BLEU score 하락이 1 미만으로 거의 없다는 점에서 대부분의 word vector를 1-bit quantization해도 성능에는 크게 영향을 주지 않는다는 것을 알 수 있다.

2. Decoder block

   평균 1.8bit quantization은 decoder의 세 sub-layer \(Dec_{dd},\ Dec_{ed},\ Dec_{ffn}\)에 각각 2, 3, 1bit를 부여한 결과이다. 이는 여러 실험을 통해 가장 적절한 값을 선택한 결과이다. decoder block에도 quantization을 수행한 후인 (2.5, 1.8, FP)의 성능은 baseline 대비 BLEU score가 대략 1 정도 하락한 수치인데, 전체 #parameters의 69%를 quantization을 했음을 생각하면 매우 미미한 수치이다.

3. Encoder block

   encoder block은 parallelizable하기 때문에 inference time에서 decoder block에 비해 비중이 낮다. 따라서 decoder block보다 많은 bit를 부여했다. 평균 #bits 3.7은 \(Enc_{ee},\ Enc_{ffn}\)에 각각 3, 4 bit를 부여한 결과이다. 주목할만한 점은 Decoder block까지 quantization을 수행했을 때 (2.5, 1.8, FP)보다 Encoder block까지 quantization을 수행했을 때 (2.5, 1.8, 3.7) BLEU score가 오히려 상승했다는 점이다. 전체 quantization이 끝나고 나면 baseline model 대비 11.8배 작은 model로 BLEU score는 단지 0.5만이 하락했음을 알 수 있다.

Inference Speed Up

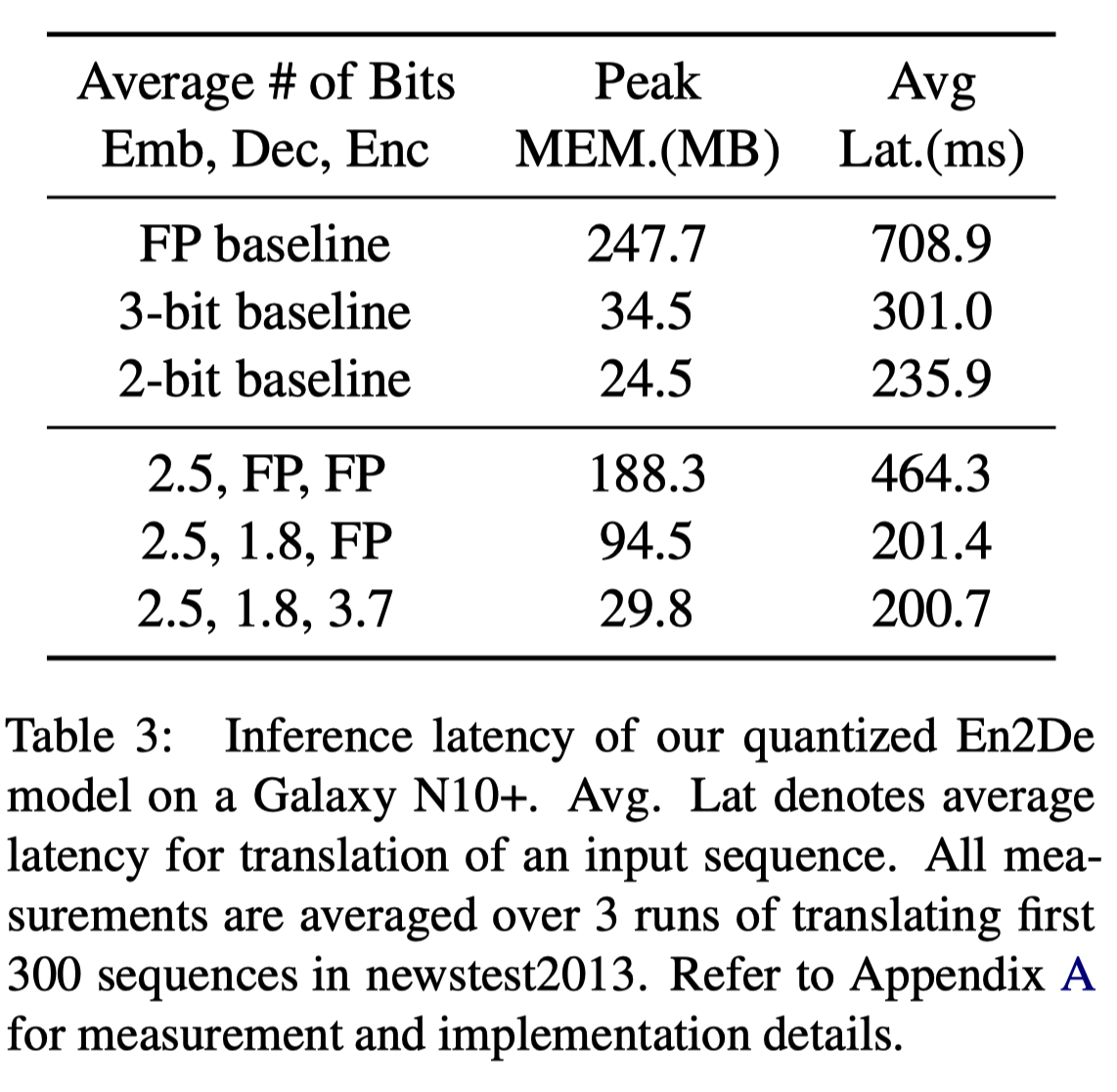
본 논문에서 제시한 2.6bit (2.5, 1.8, 3.7) model은 baseline 대비 3.5배 inference time을 보였다. 그 외에 주목할만한 점은 Encoder quantization을 수행하지 않은 11.3bit (2.5, 1.8, FP) model이 이미 2-bit baseline보다더 빠른 inference time을 보인다는 것이다. 이를 통해 실제로 inference time을 줄이기 위해서는 단순히 quantization bit를 줄이는 것보다 memory wall을 해결하는 것이 더 중요하다는 것을 알 수 있다.

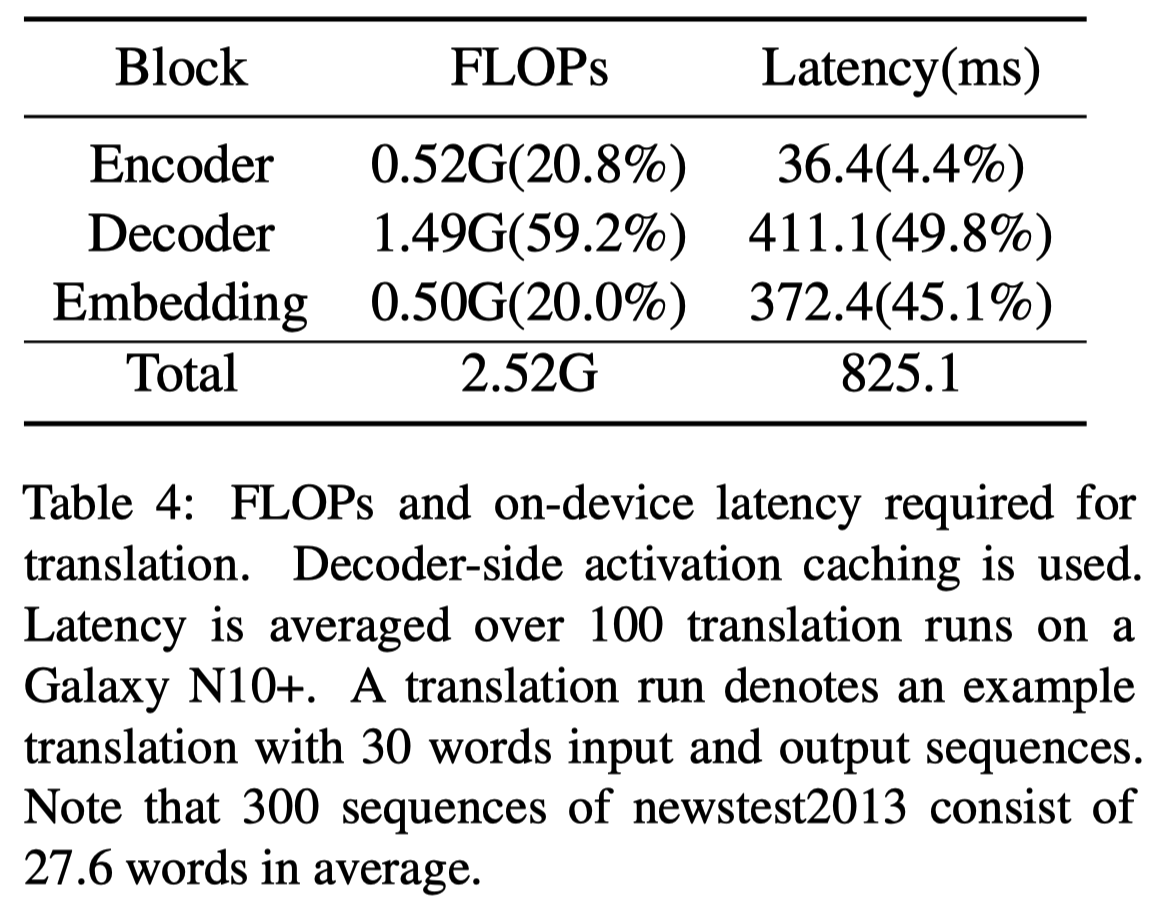
FLOP는 연산량을 의미한다. decoder block은 encoder block보다 더 많은 3배 더 많은 연산을 요구함을 확인할 수 있다. 때문에 실제 latency에서 decoder는 encoder보다 11배 많은 시간을 소모한다. embedding block 의 경우에는 연산량은 encoder block과 유사하지만 latency는 11배 더 많은 시간을 소모함을 확인할 수 있다. 이를 통해 on-device에서 inference time을 줄이기 위해서는 memory 효율성을 확보하는 것이 가장 중요함을 알 수 있다.

Comparison

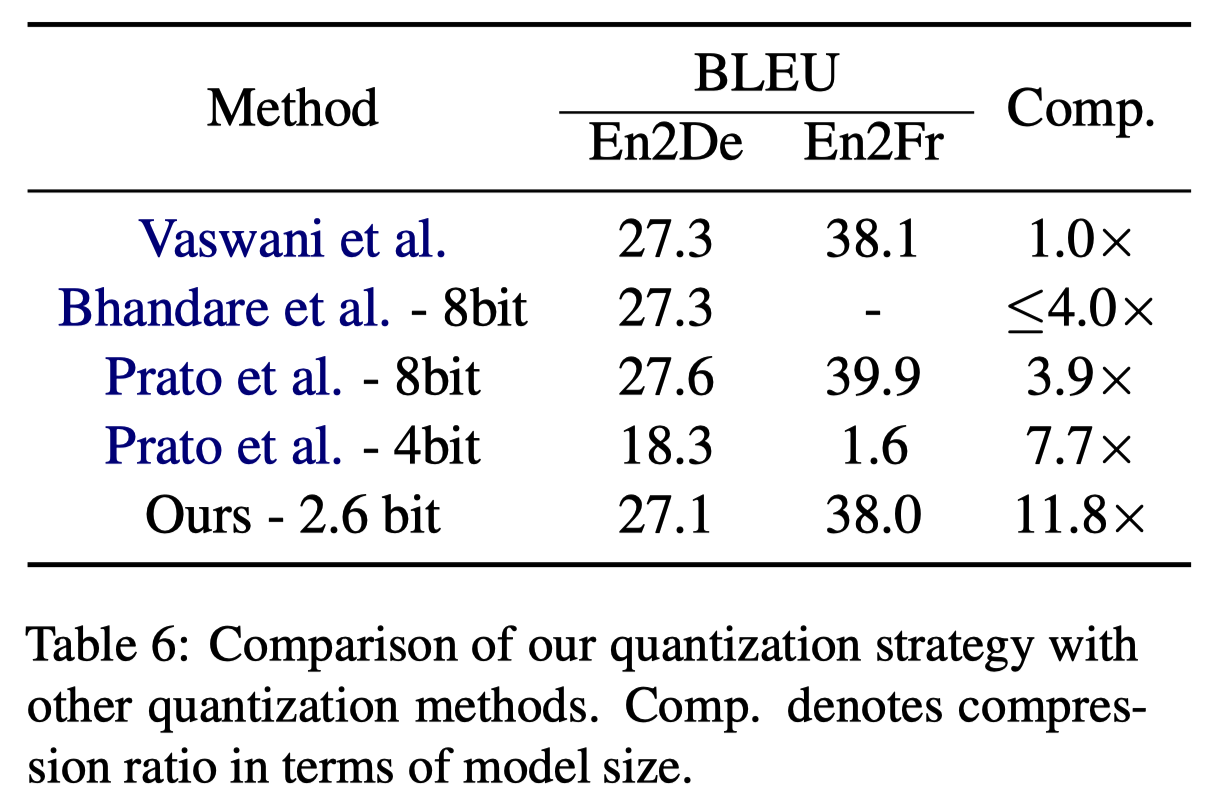
다른 Transformer quantization model과 비교했을 때 성능을 가장 잘 보존하면서도 inference time은 압도적으로 빨랐다.

Qualitative Analysis

대부분의 word에 대해 1bit로 quantize하는 본 논문의 quantization 방식이 decoder에서 다음 token을 정확하게 예측하지 못하도록 하는지 실험을 진행했다. BLEU score에서는 두드러지게 나타나지 않는 잘못된 단어 예측 현상이 발생하는지 확인하기 위해 baseline model과 2.6 bits model의 실제 번역 결과를 비교했다. 그 결과 1bit로 quantization된 단어들(밑줄친 단어들)에 대해서도 decoder는 정확히 예측함을 확인할 수 있었다.

Conclusion

Transformer에 최적화된 non-uniformed quantization 방식을 제안했다. Transformer의 각 block들(embedding, decoder, encoder)과 그 sub-layer들에 적절한 수치를 찾아 결론적으로 평균 2.6bit를 갖는 quantization 방식을 도출해냈다. 이 model은 baseline 대비 11.8배 작으며 memory 사용은 8.3배 적고, mobile device에서 3.5배 빠른 속도를 보이면서도 BLEU score는 0.5만이 감소했다.